Знаковая арифметика в Verilog
 Шауэрман Александр А. shamrel@yandex.ru
Шауэрман Александр А. shamrel@yandex.ru
Что может быть проще, сложить два числа 2 и 3? Даже если числа будут представлены в двоичном коде проблем возникнуть не должно: записываем одно число под другим и поразрядно, с учетом переноса, складываем. Все просто, курс информатики за 8 класс средней школы. Но почему-то все меняется, когда сложить требуется положительное число с отрицательным, например 2 и -3, и у многих возникает сложность, как казалось бы на пустом месте, там где ее быть не должно. В данной статье не будем рассматривать принцип представления отрицательных чисел в дополнительном коде, подразумевается, что это знакомо и понятно, а попробуем изучить на практике некоторые возможности языка Verilog по работе с знаковой арифметикой, которые позволяют существенно упростить жизнь начинающему разработчику на ПЛИС.
Чтобы не быть голословным и не ограничиваться только чтением и комментированием стандарта Verilog-2001, будем проводить эксперименты на реальной плате с ПЛИС. В качестве аппаратного обеспечения для себя я выбрал учебный стенд LESO2 последней модификации (LESO2.4). В нем есть 8 тумблеров, 8 светодиодов и одна кнопка, пожалуй, большего от него нам сейчас и не потребуется. Так как тумблеров всего восемь, будет логичным все примеры строить на четырех-битных числах. Правые четыре тумблера задают первый операнд, назовем его A, левые четыре тумблера – второй операнд B. Результат операции выведем на светодиоды.
Для того чтобы расставить все точки над i, приведу таблицу перевода десятичного числа в двоичный эквивалент.
| Десятичное значение | Двоичное значение |
|---|---|
| 7 | 4'b0111 |
| 6 | 4'b0110 |
| 5 | 4'b0101 |
| 4 | 4'b0100 |
| 3 | 4'b0011 |
| 2 | 4'b0010 |
| 1 | 4'b0001 |
| 0 | 4'b0000 |
| -1 | 4'b1111 |
| -2 | 4'b1110 |
| -3 | 4'b1101 |
| -4 | 4'b1100 |
| -5 | 4'b1011 |
| -6 | 4'b1010 |
| -7 | 4'b1001 |
| -8 | 4'b1000 |
Как видно из таблицы, признак того, что число является отрицательным – это единица в старшем разряде.
Знаковое сложение
Рассмотрим простой модуль, который складывает два 4-х битных числа, при этом помним, что при сложении двух n-битных чисел, разрядность результата будет n+1 бит:
module adder ( input [3:0] A, // Первый операнд input [3:0] B, // Второй операнд output [4:0] Sum // Результат ); assign Sum = A + B; endmodule
Для исследования модуля создадим в Quartus проект. В модуль верхнего уровня установим экземпляр модуля adder:
module signed_arithmetic ( (* chip_pin = "53, 54, 55, 58, 59, 60, 64, 65" *) input [7:0] sb_i, // Тумблеры (* chip_pin = "11, 10, 8, 7, 6, 3, 2, 1" *) output [7:0] led_o // Светодиоды ); adder adder_inst( .A(sb_i[3:0]), .B(sb_i[7:4]), .Sum(led_o[4:0]) ); endmodule
Сам исследуемый модуль можно поместить в том же файле, ниже основного. Компилируем, загружаем в стенд.
Устанавливая операнды A и B с помощью тумблеров. Легко убедиться, что сумматор дает вполне корректный результат, если оба операнда положительны, но что будет если один из них станет отрицательным? Проверим схему на двух примерах, сложим числа 1 (4'b0001) и -3 (4'b1101), 3 (4'b0011) и -3 (4'b1101).
| B | A | Sum |
|---|---|---|
| 1101 (-3) | 0001 (1) | 01110 (14) |
| 1101 (-3) | 0011 (3) | 10000 (-16) |
Не совсем то, что мы хотели бы увидеть. В первом примере такой же результат (5'b01110) даст сложение двух положительных чисел 7 (4'b0111) и 7 (4'b0111). В чем же дело? А дело в не совсем очевидной дополнительной операции, возникающей при сложении двух чисел – увеличение разрядности операндов. Когда мы складываем столбиком два числа, мы как бы подразумеваем наличие в слагаемых дополнительного старшего равного нулю разряда (выделено серым):
01101 (-3)
+ 00001 (1)
01110 (14)
Если посмотреть синтезируемую Quartus схему (Tools -> Netlist Viewers -> RTL Viewer, RTL – Register Transfer Level), то можно убедиться, что именно так и поступает компилятор:
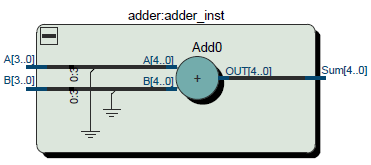
Рисунок 1 – RTL беззнакового сумматора
Старшие разряды соединены с общим проводом, на них подается ноль. Но этот старший разряд не всегда должен быть ноль! Старший разряд должен содержать признак знака, и потому, если число отрицательное, дополнено оно должно быть единицей:
11101 (-3)
+ 00001 (1)
11110 (-2)
Таким образом, следуя элементарной логике, перед сложением операнды необходимо дополнить знаковым разрядом. Решая эту задачу в лоб, изменим модуль adder следующим образом:
module adder ( input [3:0] A, input [3:0] B, output [4:0] Sum ); assign Sum = {A[3],A} + {B[3],B}; endmodule
Компилируем, смотрим RTL:
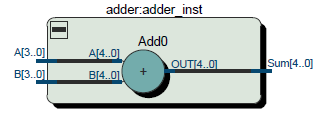
Рисунок 2 – RTL знакового сумматора
Теперь на вход сумматора подается все 5 разрядов. Загружаем, проверяем. Работа с положительными числами осталась без изменений, а вот сложение чисел из предыдущего примера дает корректный результат:
| B | A | Sum |
|---|---|---|
| 1101 (-3) | 0001 (1) | 11110 (-2) |
| 1101 (-3) | 0011 (3) | 00000 (0) |
Несмотря на работоспособность такая реализация обладает плохой масштабируемостью, а модули плохо параметризируются: представьте себе, что необходимо сложить числа различной разрядности, придется вручную вычислять и задавать длину знакового дополнения. Поэтому в Verilog начиная с версии 2001-го года, а именно эта версия используется в Quartus по умолчанию, введена поддержка знаковых операций, если для объявления A и B использовать знаковый тип, то компилятор задачу дополнения знаковыми разрядами возьмет на себя. В этом случае модуль будет иметь следующий вид:
module adder ( input signed [3:0] A, input signed [3:0] B, output signed [4:0] Sum ); assign Sum = A + B; endmodule
Нетрудно убедиться, что RTL и функционирование схемы будет точно такими же, как и в предыдущем случае (рисунок 2).
В примерах выше я использовал положительный операнд А. Может быть не обязательно порт A объявлять, как signed? Исследуем модуль:
module adder ( input [3:0] A, input signed [3:0] B, output signed [4:0] Sum ); assign Sum = A + B; endmodule
После компиляции получаем RTL как на рисунке 1, что соответствует беззнаковому сумматору. При этом не только операнд A дополнен нулем, но и операнд B. Естественно, поведение схемы описывает таблица 2. И это полностью соответствует стандарту Verilog-2001. Запомним одно важное правило, актуальное не только для операции сложения, но и для всех арифметических операций:
Если хотя бы один из операндов имеет тип unsigned, результат будет беззнаковым, независимо от остальных операндов и типа операции.
И наоборот:
Если все операнды знаковые (signed), то результат тоже будет знаковый.
Из этого правила следует еще одно очевидное правило:
Тип выражения определяется типом его операндов и не зависит от типа переменной, в которую присваивается результат.
Это значит, что в объявлении выходного порта Sum, слово signed можно опустить. На результате это не скажется, однако я не рекомендую этого делать, так как ключевое слово signed выполняет роль комментария и помогает понять логику работы модуля.
Сложение знакового и беззнакового числа
Доверить компилятору управление знаковым разрядом – это хорошая идея. Используя тип signed строить выражения на основе знаковой арифметики стало удобно, но проблема может прийти откуда ее совсем не ждали. А если нам понадобится сложить знаковое и беззнаковое число? Если следовать логике приведенных выше правил, при сложении знакового и беззнакового чисел результат будет беззнаковым.
Для решения таких задач стандартом языка предусмотрены специальные системные функции $signed() и $unsigned(). Эти функции по сути своей являются директивами компилятору, они говорят ему, как он должен интерпретировать выражение. При этом разрядность входного выражения не меняется.
$signed – возвращаемое значение знаковое,
$unsigned – возвращаемое значение беззнаковое.
Попробуем переписать модуль из предыдущего примера, где мы пытались операнд A сделать беззнаковым, с использованием функции $signed. Если мы просто применим функцию к операнду A, то это будет эквивалентно объявлению A как signed, и все значения больше 4'b0111 ('d7) окажутся отрицательными, так как старший бит будет равен единице. Чтобы этого не произошло, вручную дополним старший бит нулем:
module adder ( input [3:0] A, input signed [3:0] B, output [4:0] Sum ); assign Sum = $signed({1'b0, A}) + B; endmodule
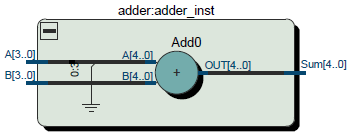
Рисунок 3 – RTL сумматора. A – беззнаковый, B – знаковый
Как видно из RTL, старший бит операнда A всегда равен нулю, а операнд B остался знаковым. Операнд A может принимать только положительные значения в соответствии со своей разрядностью: от 0 и до 15, а операнд B может быть от -8 до 7. Так как разрядность выхода так и осталась 5 бит, диапазон значений Sum: от -16 и до 15. Потому, несмотря на то, что такой сумматор корректно работает, может возникнуть переполнение, если результат должен получиться более 15.
Загрузим в ПЛИС, помимо уже привычных нам примеров (-3+1 и -3+3) добавим еще несколько, чтобы продемонстрировать новые свойства.
| B знаковый |
A беззнаковый |
Sum знаковый |
Комментарии |
|---|---|---|---|
| 1101 (-3) | 0001 (1) | 11110 (-2) | Числа из предыдущих примеров. Ничем не примечательны. Работает корректно. |
| 1101 (-3) | 0011 (3) | 00000 (0) | То же. |
| 1101 (-3) | 1000 (8) | 00101 (5) | A превышает максимальное допустимое положительное число для знакового типа разрядностью 4. Результат корректен. |
| 0111 (7) | 1000 (8) | 01111 (15) | B – максимальное допустимое положительное число. Sum принял максимально допустимое значение. Результат корректен. |
| 0111 (7) | 1001 (9) | 10000 (-16) | При сложении двух положительных чисел получили отрицательное. Переполнение! |
Логика признака переполнения основана на свойствах дополнительного кода. Можно утверждать, что произошло переполнение, если старший знаковый бит изменился вопреки знаку операндов и характеру операции. Например, сложение двух положительных чисел должно давать положительный результат, а если получилось иначе, то имеет место переполнение. Но на практике часто делают иначе, увеличивают разрядность результата и смотрят, не переписали ли значащие разряды знаковый.
module adder ( input [3:0] A, input signed [3:0] B, output signed [4:0] Sum, output overflow ); wire sign; assign {sign, Sum} = $signed({1'b0, A}) + B; assign overflow = sign^Sum[4]; endmodule
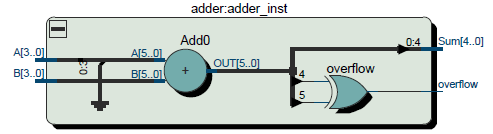
Рисунок 4 – RTL cумматора с флагом переполнения
Сумматор с переносом
Типичный пример сложения смешанных типов – это сумматор, который должен учитывать флаг переноса. Флаг переноса представляет собой такой же полноценный операнд как A и B, только состоит всего из одного бита, принимает значение либо 0, либо 1. Ни о каком знаке в однобитном числе и речь идти не может. Получается тип у флага переноса будет беззнаковый, а это значит, результат сложения тоже будет беззнаковым. Для решения задачи воспользуемся приемом из предыдущего пункта: дополним вход переноса нулем и преобразуем к знаковому типу:
module adder ( input signed [3:0] A, input signed [3:0] B, input carry_in, output signed [4:0] Sum ); assign Sum = A + B + $signed({1'b0, carry_in}); endmodule
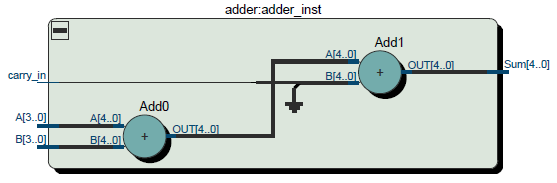
Рисунок 5 – RTL сумматора с переносом
Для того, чтобы испытать модуль на учебном стенде, нам понадобится в модуль верхнего уровня добавить еще один вход – вход тактовой кнопки. Его мы будем использовать в качестве входа переноса. Кнопка работает с инверсией: если отпущена, то на входе будет логическая единица, если нажата, то ноль. Для удобства при установке экземпляра модуля учтем и это. Ниже на листинге показан исходный код модуля верхнего уровня:
module signed_arithmetic( (* chip_pin = "53, 54, 55, 58, 59, 60, 64, 65" *) input [7:0] sb_i, // тумблеры (* chip_pin = "52" *) input sw_i, // кнопка (* chip_pin = "11, 10, 8, 7, 6, 3, 2, 1" *) output [7:0] led_o // светодиоды ); adder adder_inst( .A(sb_i[3:0]), .B(sb_i[7:4]), .carry_in(~sw_i), .Sum(led_o[4:0]) ); endmodule
Компилируем, загружаем, убеждаемся, что модуль работает верно: к результату сложения операндов A и B (устанавливаются тумблерами) прибавляется единица, если кнопка нажата.
Знаковое перемножение
Разрядность результат перемножения двух n-битных значений равно 2n. По аналогии со сложением, в начале разберемся, как выполнить операцию умножения в столбик. Второй множитель (второй операнд) рассматривается побитно, начиная с младшего значимого бита, если бит равен единице, то первый множитель сдвигается влево на число позиций, равных весу текущего бита второго множителя и прибавляется к результату. При этом, если операция беззнаковая, то слева слагаемые дополняются нулем (дополнительные элементы показана серым):
1101 (-3)
* 0010 (2)
00000000
+ 00011010
+ 00000000
+ 00000000
00011010 (26)
Если операция знаковая, то дополняется знаковым битом:
1101 (-3)
* 0010 (2)
00000000
+ 11111010
+ 00000000
+ 00000000
11111010 (-6)
В первом случае 4'b1101 (-3) было интерпретировано не как отрицательное число, а как положительное 13, потому и произведение получилось 26. Во втором случае, получен корректный результат с точки зрения знаковой арифметики.
Реализовать такой сумматор на языке Verilog достаточно просто, сделаем модуль по аналогии с сумматором:
module multipliers ( input signed [3:0] A, input signed [3:0] B, output signed [7:0] Mult ); assign Mult = A * B; endmodule
Компилируем, смотрим RTL:
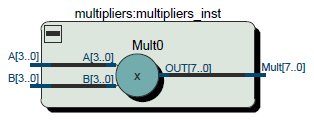
Рисунок 6 – RTL знакового умножителя
Загружаем в ПЛИС, проверяем, результат исследования сведем в таблицу:
| B знаковый |
A знаковый |
Mult знаковый |
Комментарий |
|---|---|---|---|
| 1101 (-3) | 0010 (2) | 1111 1010 (-6) | Числа из вычисления столбиком. Умножаем отрицательное число на положительное. Результат имеет отрицательный знак. |
| 0011 (3) | 0010 (2) | 0000 0110 (6) | Произведение двух положительных чисел. Результат положительный. |
| 0111 (7) | 0111 (7) | 0011 0001 (49) | Произведение двух самых больших положительных чисел из допустимого диапазона. Результат корректен. |
| 1000 (-8) | 1000 (-8) | 0100 0000 (64) | Произведение двух самых маленьких отрицательных чисел. Результат – корректное положительное число. |
Если требуется умножить знаковое число на беззнаковое, дополним беззнаковый операнд нулем и преобразуем к знаковому типу:
module multipliers ( input [3:0] A, input signed [3:0] B, output signed [7:0] Mult ); assign Mult = $signed({1'b0, A}) * B; endmodule
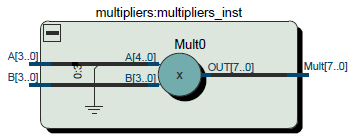
Рисунок 7 – RTL умножителя. Вход A – беззнаковый, вход B – знаковый
Как и раньше, результат исследования сведем в таблицу:
| B знаковый |
A беззнаковый |
Mult знаковый |
Комментарии |
|---|---|---|---|
| 1101 (-3) | 0010 (2) | 1111 1010 (-6) | |
| 0011 (3) | 0010 (2) | 0000 0110 (6) | |
| 1000 (-8) | 1000 (8) | 1100 0000 (-64) | Числа из предыдущего примера. Но теперь умножается отрицательное число на положительное, поэтому результат отрицателен. |
| 0111 (7) | 1111 (15) | 0110 1001 (105) | Произведение двух самых больших положительных чисел из допустимого диапазона. Результат корректен. |
Небольшие советы
1. Результат сцепления (Concatenation) всегда дает беззнаковый результат. Потому в предыдущих примерах, при ручном добавлении знакового разряда к флагу переноса, приходилось применять функцию $signed для получения знакового типа. Отсюда пара полезных приемов. Для получения самого большого положительного числа разрядности N можно поступить так:
wire signed [N-1:0] max = $signed({1'b0,{(N-1){1'b1}}});
А самое маленькое отрицательное число (самое большое по модулю):
wire signed [N-1:0] min = $signed({1'b1,{(N-1){1'b0}}});
2. Выборка из вектора одного или нескольких бит всегда будет беззнаковой. Результат будет беззнаковым даже если выбрать вектор полностью. Для примера выведем на светодиоды значение min, но для эксперимента разрядность min выберем меньше восьми:
wire signed [5:0] min = $signed({1'b1,{5{1'b0}}}); // 6'b100000 (-32) assign led_o = min; // разрядность led_o – восемь
В результате на светодиоды выведется значение 1110 0000. При присвоении знакового числа знаковый разряд заполнил дополнительные биты, произошло знаковое расширение числа до разрядности приемника. Значение -32 сохранилось. Теперь проделаем, казалось бы, тоже самое, но с помощью выборки из вектора min:
wire signed [5:0] min = $signed({1'b1,{5{1'b0}}}); // 6'b100000 (-32) assign led_o = min[5:0]; // разрядность led_o – восемь
Выборка min[5:0] дала беззнаковый результат, и, как следствие, на светодиодах положительное значение 0010 0000 (32).
3. Уверен, как задавать беззнаковую константу всем известно. По аналогии можно задавать знаковые положительные и отрицательные константы:
-8'd11 // Можно поставить знак минус перед числом, 8'd-11 // а вот так будет не верно. -8'h0B // То же самое, только в шестнадцатеричной форме, 8'shF6 // Дополнительный символ "s" указывает на то, что число // должно интерпретироваться как знаковое. -8'b00001011 // То же самое, но в двоичной форме. 8'sb11110101 // То же значение, но с помощью "s".
4. При разработке на ПЛИС часто встречается конструкция с тернарным оператором выбора:
assign led_o = ( <условие> ) ? 0 : (A + B); // беззнаковый результат
При такой записи, даже если операторы A и B будут объявлены как знаковые, результат операции будет беззнаковым! Это довольно распространенная ошибка. Но это полностью соответствует правилу: если хотя бы один из операторов в выражении unsigned, то и результат unsigned. В данном случае учитывается беззнаковый тип константы 0 и достаточно явно указать константе 0 ее знаковость, например, так 'sh0, и все станет на свои места:
assign led_o = ( <условие> ) ? 'sh0 : (A + B); // знаковый результат
Вместо заключения
Приведу краткий свод правил, памятку по работе с знаковым типом.
1. Результат сцепления будет беззнаковым, независимо от типа операндов.
2. Результат выборки одного или нескольких бит из вектора будет беззнаковым.
3. Для приведения выражения к знаковому типу используется системная функция $signed.
4. Для приведения выражения к беззнаковому типу используется системная функция $unsigned.
5. Результат сравнения имеет беззнаковый тип.
6. Если хотя бы один из операндов имеет беззнаковый тип (unsigned), результат будет беззнаковым, независимо от остальных операндов и типа операции. Если все операнды знаковые (signed), то результат тоже будет знаковый.
7. Тип выражения определяется только типом операторов и не зависит от типа переменной, которому это значение присваивается.
8. При записи знаковых констант можно воспользоваться дополнительным символом "s".
Литература
1. IEEE Standard Verilog Hardware Description Language, IEEE Computer Society, IEEE, New York, NY, IEEE Std 1364-2001.


